Published as part of the Financial Stability Review, May 2022.
Synthetic leverage has become an important feature of the financial system. It refers to the exposure embedded in derivative contracts. These instruments enable market participants to take on synthetic market exposure, sometimes at little cost (for certain types of derivatives and underlying assets), and allow them to amplify gains at the risk of magnifying losses. Leverage tends to be less strictly regulated in parts of the non-bank financial sector than it is for banks, and non-bank institutions are able to increase leverage synthetically at little cost. During events such as the failure of Long-Term Capital Management and the collapse of AIG, and more recently Archegos, losses on derivative exposures spread to bank counterparties.
There are multiple ways of measuring the amount of leverage in the financial system. Traditional leverage ratios at entity level do not fully capture the contingent commitments associated with derivative positions, as future gains and losses can substantially exceed the market value at which derivatives are recorded on the balance sheet. A generally accepted method used to capture synthetic leverage applies the concept of cash-equivalent portfolios,[2] which also forms the basis of leverage metrics in EU fund regulation.[3] Another approach, which is the focus of this box, considers the derivative contracts themselves and assesses the extent to which such contracts can be used to take positions which embed leverage.[4]
This box explores the link between synthetic leverage and margining from two angles. First, we look at the ratio of derivatives’ gross notional value (GNV) to initial margins (IMs) posted, which may be viewed as the level of synthetic leverage in a particular type of contract.[5] Low levels of IMs allow financial institutions to increase their market exposure via derivatives with very little initial funding. During periods of elevated price volatility, IMs tend to increase relative to the GNV – this offers the benefit of better protection against counterparty risk in stressed market conditions. However, this can also intensify liquidity needs in a procyclical manner and create incentives for deleveraging, which could contribute to the amplification of price declines. Second, we calculate the ratio of the daily absolute flows of variation margins (VMs) to IMs, which may be seen as a proxy for the amplification of profits and losses on a derivative portfolio.[6] For a highly leveraged portfolio, this ratio would increase more in times of high market volatility. Daily ratios greater than 1 suggest – ex post – that the capital committed as IM would not have been sufficient to fully protect against losses if the counterparty had failed. These two metrics are calculated for portfolios of equity derivatives held by non-bank financial institutions to capture risks similar those faced by Archegos.[7]
The high GNV/IM multipliers for equity derivatives suggest that these instruments could entail potentially high leverage-like risk. Multipliers range between 10 and 80 across instruments during most of the period covered, with equity options displaying the largest multipliers (Chart A, panel a). Although the GNV/IM ratio decreased for equity futures during the March 2020 market turmoil, it did not decline significantly for swaps and options, the difference probably stemming from the models used to calculate IMs.[8] Following this episode, the GNV/IM ratio for both options and futures rose throughout most of 2020 and 2021, with the increase accelerating in the fourth quarter of 2021.The increase in the ratio for options seems to have been driven by a decrease in IMs as the associated GNV remained relatively stable during this period. The GNV/IM ratio for swaps was relatively stable.
The ratios between daily absolute VM flows and IMs at the instrument level increased significantly in March 2020, reaching over 1 for some NBFIs (Chart A, panel b). While the majority of NBFIs posted more IM than the amount of VM calls, for a significant number of non-banks VM calls exceeded IM during the March 2020 market turmoil, suggesting that some counterparties would not have been fully covered by IM if the other counterparty had defaulted. Focusing on NBFIs with high exposures to market volatility, the median VM/IM ratio in the top 20th percentile ranged from 1.7 to 2.5 during March 2020 across all instruments considered. The significant rise of VM calls also points to potential liquidity stress arising from derivative positions. The median ratio for futures and options also increased in February and March 2022, reflecting higher volatility, although the levels reached were not comparable with those of March 2020. This also reflected the fact that recent events had affected energy and commodity derivatives to a greater extent than equity derivatives.
Chart A
The GNV/IM ratio is a proxy for the synthetic leverage of a derivative portfolio, while the VM/IM ratio captures the amplification of profit and losses at the portfolio level
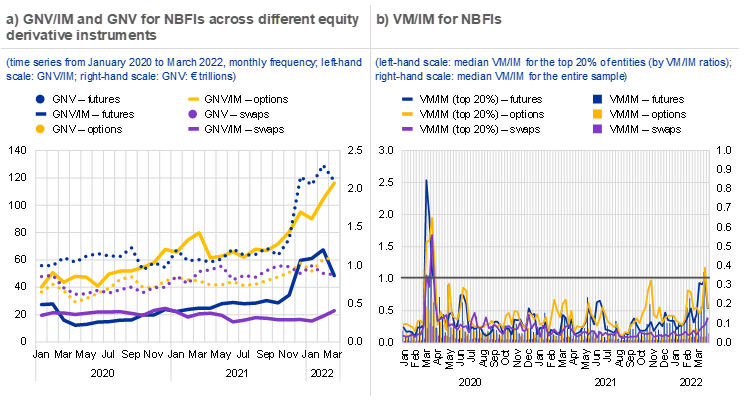
Sources: ECB (European Market Infrastructure Regulation) and authors’ calculations.
Notes: Non-bank financial institutions (NBFIs) have been identified through internal sector enrichment classification codes.[9]
In panel a), the GNV/IM ratio is computed for derivative portfolios containing only equities as underlying instruments. Mixed portfolios containing asset classes other than equities have been excluded from the sample. Consequently, GNV and IM in the charts do not represent the exposure of NBFIs to all equity derivative positions. Coverage ranges from 60% to 80% in terms of the overall notional over time.
In panel b), ratios are computed at the entity level for all NBFIs transacting futures, options and swaps on equities. Very small positions characterised by zero margin posted and low levels of notional have not been considered for the computation of leverage.
Leverage risk can materialise through margin calls and uncovered counterparty exposure during periods of high market volatility. One of the key risks associated with leverage embedded in derivative portfolios is the resulting procyclical margin calls during periods of market stress. Moreover, the IM might not always be sufficient to cover possible counterparty risk in times of very high market volatility. Higher levels of IM in quieter periods could be beneficial from a financial stability perspective as they could reduce the procyclicality of margin calls, as well as leverage-like risk in derivative portfolios. However, there are trade-offs to consider, including the possible indirect impact derivatives may have on users through higher liquidity and funding needs.[10]
The authors express their gratitude to Linda Fache Rousová and Lorenzo Cappiello for their contributions and valuable feedback.
See Breuer, P., “Measuring off-balance-sheet leverage”, Journal of Banking and Finance, Vol. 26 (2-3), 2002, pp. 223-242.
For example, the “commitment approach” in the Undertakings for Collective Investment in Transferable Securities (UCITS) Directive and the Alternative Investment Fund Managers Directive (AIFMD). Other common metrics include gross notional over net asset value and value-at-risk concepts. See the box entitled “Synthetic leverage in the investment fund sector”, Financial Stability Review, ECB, May 2015.
See Frazzini, A. and Pedersen, L.H., “Embedded Leverage”, NBER Working Papers, No 18558, November 2012.
This recalls the standard definition of the leverage ratio, which is market exposure (the GNV captures the synthetic market exposure) over unit of committed capital (here represented by IMs).
By definition, the leverage ratio amplifies returns on equity: .
Gross notional and margin data are obtained from the EMIR dataset. The sample comprises a broad range of institutions including investment funds, pension funds, insurance companies and other financial institutions. The bulk of such derivatives are held by investment funds.
The differences between the models used to compute IMs depend heavily on the calibration choices made by central counterparties (for centrally cleared transactions – mostly options and futures in our sample) or counterparties (for non-centrally cleared transactions – swaps in our sample). In particular, the models used by the latter are less responsive to short-term fluctuations in market volatility. For further information, see the box entitled “Lessons learned from initial margin calls during the March 2020 market turmoil”, Financial Stability Review, ECB, November 2021.
See Lenoci, F.D. and Letizia, E, “Classifying Counterparty Sector in EMIR Data”, in Consoli, S., Reforgiato Recupero, D. and Saisana, M. (eds.), Data Science for Economics and Finance, Springer, 2021.
See Section 5.2 for a broader discussion of policies used to address leverage risk in the non-bank financial sector.


